Самое актуальное и обсуждаемое
Популярное
Полезные советы

Важно знать!
Кто такой логист и чем он занимается? популярность, обязанности и требования к профессии
Должностная инструкция
Все навыки и знания, которыми должен обладать операционный логист, более подробно прописаны в должностной инструкции. Согласно этому документу, специалист в области логистики должен...
Читать далее
Проверка контрагента: онлайн-сервисы и офлайн-методы
Такси везет москва
Услуги переезда под ключ: перевозим картины, корзины, картонки…
Как сделать из типового листинга крутую хаб-страницу? делаем всё правильно, ранжируемся выше и увеличиваем конверсию
Что такое транспорт
Цмрбанк
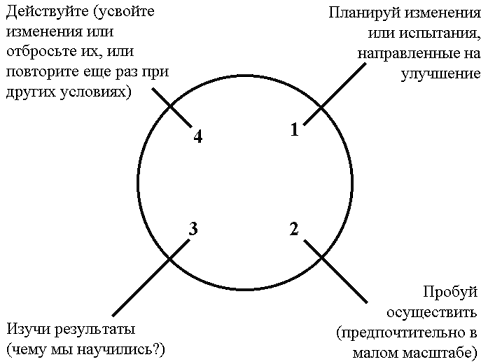
Кайдзен
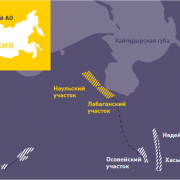
Транспортная логистика
Складская логистика: понятие, принципы, функции, задачи. организация складской логистики
Рекомендуем
0
Лучшее

Важно знать!
Икеа белая дача в москве
IKEA МЕГА Белая Дача на карте - проложить маршрут
На нашем сайте вы сможете проложить маршрут от вашего местоположения к магазину МЕГА ИКЕА Белая Дача без каких либо трудностей....
Читать далее
Организация переезда офиса
Что такое принцип парето: объяснение, примеры, значение
Карго доставка из китая
Грузовое такси газелькин: номер телефона, тарифы, промокоды, автопарк, условия работы
Кросс-докинг- это что? кросс-докинг: склад, схема, услуги
Лайфхак: как растаможить машину из армении, казахстана, германии и абхазии в россии
Игры грузовики
Перевозка грузов из россии в казахстан
Воздушный транспорт. воздушный транспорт — вид транспорта, производящий перевозку грузов и пассажиров воздушным путем с помощью летательных аппаратов: — презентация
Новое
Обсуждаемое

Важно знать!
Перевозка спецтехники тралом по россии и в москве
Перевозка сельхозтехники
Транспортировка сельхозтехники – достаточно востребованная услуга, особенно накануне начала посевной кампании или перед уборкой урожая. Перевозка негабаритных комбайнов и тракторов,...
Читать далее
Какие бывают размеры паллет. размеры стандартных и евро-паллет (поддонов)
Правила перевозки скоропортящихся продуктов и грузов
Перевозка грузов до 10 тонн в россии
Анализ страницы вконтакте
Единая диспетчерская жкх москвы
Как можно исправить ошибки, связанные с msiservice.exe?
Перевозка лодки: способы транспортировки лодок пвх, примеры
Юлия лазарева
Расходная накладная
Популярное
Актуальное

Важно знать!
Вакансии экспедиторов в железнодорожном
«Не угадаешь, во сколько начнется бум»
Пока многие офисы еще «раскачиваются» перед началом дня, на складе «Е-доставки» уже вовсю кипит работа. Мы приезжаем в Большое Стиклево к девяти утра, но заявки...
Читать далее
Перевозка животных по россии правила. рассказываем как взять своего питомца в путешествие
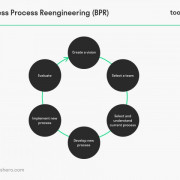
Процессный подход
Привлечение клиентов через каналы продаж
Стоимость обучения допог
Как правильно перевозить холодильник: лежа или стоя
Перевозки газелью в королеве
Какие особенности имеет договор аренды транспортного средства с экипажем
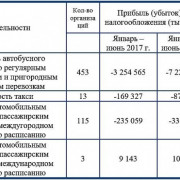
Учёт издержек обращения и их роль в бухгалтерии
Виды и правила буксировки автомобиля согласно пдд
Обновления
 Статьи
ЖД контейнеры: новая волна в грузоперевозках и логистике!
Статьи
ЖД контейнеры: новая волна в грузоперевозках и логистике!
В эру стремительно развивающейся глобальной экономики и постоянного увеличения объемов грузоперевозок...
 Статьи
Импорт и экспорт грузов в Россию: Международные авиаперевозки
Статьи
Импорт и экспорт грузов в Россию: Международные авиаперевозки
В условиях современной глобализации, мировая экономика функционирует как огромная система...
 Статьи
Процесс пожарной сертификации и организации: всё о сертификации продукции
Статьи
Процесс пожарной сертификации и организации: всё о сертификации продукции
Пожарная сертификация продукции - это важный этап в обеспечении безопасности и соответствия изделий...
 Статьи
Продукция и стандарты: Евразийский союз и российское законодательство
Статьи
Продукция и стандарты: Евразийский союз и российское законодательство
В современном мире, который все более интегрируется в глобальную экономику, стандартизация...
 Статьи
ISO-свидетельства: Ключ к Качеству и Доверию в Бизнесе
Статьи
ISO-свидетельства: Ключ к Качеству и Доверию в Бизнесе
Свидетельства ISO (Международной организации по стандартизации) представляют собой мощный инструмент,...
 Статьи
Инновации в картонной упаковке: Экологичные методы и материалы при изготовлении упаковки
Статьи
Инновации в картонной упаковке: Экологичные методы и материалы при изготовлении упаковки
В современном мире, где охрана окружающей среды становится все более актуальной задачей, инновации...
 Статьи
Улучшите организацию и пространство с шкафами-купе: практичность и стиль в одном!
Статьи
Улучшите организацию и пространство с шкафами-купе: практичность и стиль в одном!
Преимущества шкафов-купе: удобство, функциональность и стиль для вашего интерьера
Шкафы-купе – это...
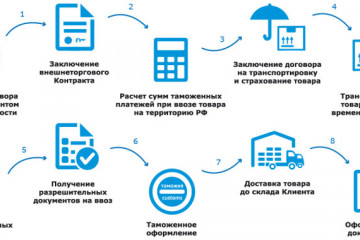 Статьи
Управление рисками в транспортной логистике: услуги страхования и защиты грузов от международных поставщиков
Статьи
Управление рисками в транспортной логистике: услуги страхования и защиты грузов от международных поставщиков
Стратегии и подходы международных поставщиков логистических услуг: эффективная интеграция и оптимизация...
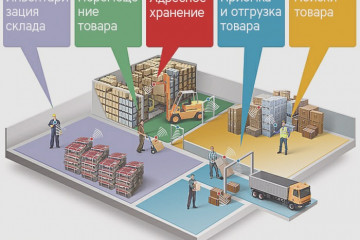 Статьи
Топ-10 самых дешевых транспортных компаний по россии
Статьи
Топ-10 самых дешевых транспортных компаний по россии
Логистические операции и перевозки являются неотъемлемыми компонентами любого успешного бизнеса. Поскольку...
 Статьи
Международные перевозки грузов
Статьи
Международные перевозки грузов
Доставка из Китая сборных грузов
Для малого/среднего бизнеса, а также физлиц генеральные перевозки...
 Статьи
Футболка-поло
Статьи
Футболка-поло
Детская одежда из России
При поиске детской одежды для поло важно учитывать, какой стиль вы хотите...
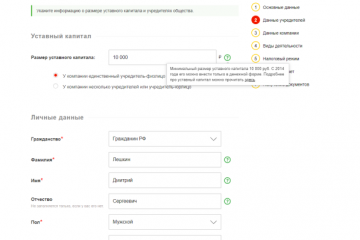 Статьи
Как зарегистрировать ооо онлайн через налоговую
Статьи
Как зарегистрировать ооо онлайн через налоговую
Регистрация ООО требует обязательного обозначения «Вид экономической деятельности», сделать это можно...